My main research focus is on designing, analyzing and implementing scalable, robust and efficient nonlinear optimization algorithms.
Research Interests
Unconstrained Nonlinear Optimization Algorithms
Aggregated Quasi-Newton Methods
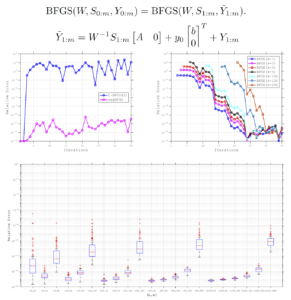
A displacement aggregation strategy is proposed for the curvature pairs stored in a limited-memory BFGS method such that the resulting (inverse) Hessian approximations are equal to those that would be derived from a full-memory BFGS method. This means that, if a sufficiently large number of pairs are stored, then an optimization algorithm employing the limited-memory method can achieve the same theoretical convergence properties as when full-memory (inverse) Hessian approximations are stored and employed, such as a local superlinear rate of convergence under assumptions that are common for attaining such guarantees. To the best of our knowledge, this is the first work in which a local superlinear convergence rate guarantee is offered by a quasi-Newton scheme that does not either store all curvature pairs throughout the entire run of the optimization algorithm or store an explicit (inverse) Hessian approximation.
Paper
- Albert S. Berahas, Frank E. Curtis and Baoyu Zhou. Limited-Memory BFGS with Displacement Aggregation. Mathematical Programming, 2021, DOI: 10.1007/s10107-021-01621-6. (Download PDF, MAPR Online)
Talks
- (postponed due to COVID-19) DataX Workshop (September 2020): Old and New Open Questions in Optimization, Princeton University, Princeton, NJ.
- ICCOPT 2019, International Conference on Continuous Optimization, Berlin, Germany. (slides)
- Numerical Analysis and Scientific Computing Seminar, November 2019, Courant Institute of Mathematical Sciences, New York University, New York, NY. (slides)
Global Convergence Rate Analysis of a Generic Line Search Algorithm with Noise
In this work, we develop convergence analysis of a modified line search method for objective functions whose value is computed with noise and whose gradient estimates are inexact and possibly random. The noise is assumed to be bounded in absolute value without any additional assumptions. We extend the framework based on stochastic methods from [Cartis & Scheinberg, 2018] which was developed to provide analysis of a standard line search method with exact function values and random gradients to the case of noisy function. We introduce a condition on the gradient which when satisfied with some sufficiently large probability at each iteration, guarantees convergence properties of the line search method. We derive expected complexity bounds for convex, strongly convex and nonconvex functions.
Paper
- Albert S. Berahas, Liyuan Cao and Katya Scheinberg. Global Convergence Rate Analysis of a Generic Line Search Algorithm with Noise. SIAM Journal on Optimization, 2021, 31(2), pp. 1489-1518. (Download PDF, SIOPT Online)
Talks
- (virtual) INFORMS Annual Meeting 2020, Institute for Operations Research and the Management Sciences Conference, National Harbor, MD. (slides)
- (postponed due to COVID-19) SIOPT 2020, SIAM Conference on Optimization, Hong Kong.
- Joint Mathematics Meetings (JMM) 2020, Denver, CO. (slides)
- Young Researchers Workshop 2019, ORIE, Cornell University, Ithaca, NY. (slides)
Constrained Stochastic Optimization
Sequential Quadratic Optimization for Nonlinear Equality Constrained Stochastic Optimization
Sequential quadratic optimization algorithms are proposed for solving smooth nonlinear optimization problems with equality constraints. The main focus is an algorithm proposed for the case when the constraint functions are deterministic, and constraint function and derivative values can be computed explicitly, but the objective function is stochastic. It is assumed in this setting that it is intractable to compute objective function and derivative values explicitly, although one can compute stochastic function and gradient estimates. As a starting point for this stochastic setting, an algorithm is proposed for the deterministic setting that is modeled after a state-of-the-art line-search SQP algorithm, but uses a stepsize selection scheme based on Lipschitz constants (or adaptively estimated Lipschitz constants) in place of the line search. This sets the stage for the proposed algorithm for the stochastic setting, for which it is assumed that line searches would be intractable. Under reasonable assumptions, convergence (resp.,~convergence in expectation) from remote starting points is proved for the proposed deterministic (resp.,~stochastic) algorithm. The results of numerical experiments demonstrate the practical performance of our proposed techniques.
Papers
- Albert S. Berahas, Frank E. Curtis, Daniel P. Robinson and Baoyu Zhou. Sequential Quadratic Optimization for Nonlinear Equality Constrained Stochastic Optimization. SIAM Journal on Optimization, 2021, 31(2), pp. 1352-1379. (Download PDF, SIOPT Online)
- (Status: Submitted) Albert S. Berahas, Frank E. Curtis, Michael J. O’Neill and Daniel P. Robinson. A Stochastic Sequential Quadratic Optimization Algorithm for Nonlinear Equality Constrained Optimization with Rank- Deficient Jacobians. arXiv preprint arXiv:2106.13015, 2021. (Download PDF)
Talks
- (upcoming, virtual) OR Colloquium, Penn State, Department of Industrial and Manufacturing Engineering.
- (upcoming, virtual) INFORMS 2019, Institute for Operations Research and the Management Sciences Conference, Anaheim, CA.
- (virtual) SIOPT 2021, SIAM Conference on Optimization, Spokane, WA. (slides)
- (virtual) EUROPT 2021, 18th Workshop on Advances in Continuous Optimization, Toulouse, France. (slides)
- (virtual) Statistics Seminar, UW Madison, Department of Statistics. (slides)
- (virtual) 3rd IMA and OR Society Conference on Mathematics of Operational Research. (slides)
Optimization Algorithms for Machine Learning
Sampled Quasi-Newton Methods
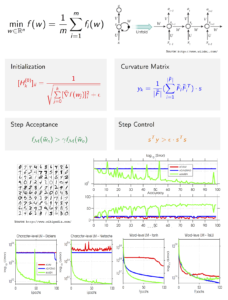
In this work, we present two sampled quasi-Newton methods for deep learning: sampled LBFGS (S-LBFGS) and sampled LSR1 (S-LSR1). Contrary to the classical variants of these methods that sequentially build Hessian or inverse Hessian approximations as the optimization progresses, our proposed methods sample points randomly around the current iterate at every iteration to produce these approximations. As a result, the approximations constructed make use of more reliable (recent and local) information, and do not depend on past iterate information that could be significantly stale. Our proposed algorithms are efficient in terms of accessed data points (epochs) and have enough concurrency to take advantage of parallel/distributed computing environments. We provide convergence guarantees for our proposed methods. Numerical tests on a toy classification problem as well as on popular benchmarking neural network training tasks reveal that the methods outperform their classical variants and are competitive with state-of-the-art first-order methods such as ADAM. We also develop a distributed variant of the S-LSR1 method (DS-LSR1). Contrary to a naive distributed implementation, DS-LSR1 drastically reduces the amount of data communicated at every iteration, has favorable work-load balancing across nodes and is matrix-free and inverse-free. The method scales well in terms of both the dimension of the problem and the number of data points. We illustrate the performance of DS-LSR1 on standard neural network training tasks.
Papers
- (Status: Coming soon!) Albert S. Berahas, Majid Jahani and Martin Takáč. Fast, Stochastic and Adaptive Sampled Quasi-Newton Methods.
- (Status: Accepted, Optimization Methods & Software) Albert S. Berahas, Majid Jahani, Peter Richtárik and Martin Takáč. Quasi-Newton Methods for Machine Learning: Forget the Past, Just Sample. (Download PDF)
- Majid Jahani, Mohammadreza Nazari, Sergey Rusakov, Albert S. Berahas and Martin Takáč. Scaling Up Quasi-Newton Algorithms: Communication Efficient Distributed SR1. 6th Annual Conference on Machine Learning, Optimization and Data Science (LOD), 2020.(Download PDF)
- Albert S. Berahas, Majid Jahani and Martin Takáč. Sampled Quasi-Newton Methods for Deep Learning. OPT 2019: Optimization for Machine Learning Workshop (NeurIPS 2019) (Download PDF)
Talks
- (postponed due to COVID-19) MDS 2020: SIAM Conference on Mathematics of Data Science, Cincinnati, OH.
- INFORMS 2019, Institute for Operations Research and the Management Sciences Conference, Seattle, WA. (slides)
Deterministic and Stochastic Hybrid Methods
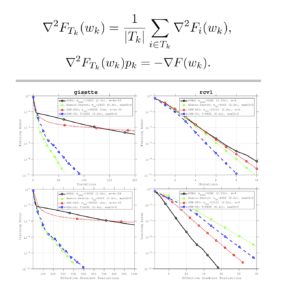
This work presents a new algorithm for empirical risk minimization. The algorithm bridges the gap between first- and second-order methods by computing a search direction that uses a second-order-type update in one subspace, coupled with a scaled steepest descent step in the orthogonal complement. To this end, partial curvature information is incorporated to help with ill-conditioning, while simultaneously allowing the algorithm to scale to the large problem dimensions often encountered in machine learning applications. Theoretical results are presented to confirm that the algorithm converges to a stationary point in both the strongly convex and nonconvex cases. A stochastic variant of the algorithm is also presented, along with corresponding theoretical guarantees. Numerical results confirm the strengths of the new approach on standard machine learning problems.
Papers
- (Status: Coming soon!) Majid Jahani, Mohammadreza Nazari, Rachael Tappenden, Albert S. Berahas and Martin Takáč. Deterministic and Stochastic Hybrid Methods.
- (Status: Coming soon!) Majid Jahani, Mohammadreza Nazari, Rachael Tappenden, Albert S. Berahas and Martin Takáč. An Adaptive Stochastic Hybrid Method for Machine Learning.
- Majid Jahani, Mohammadreza Nazari, Rachael Tappenden, Albert S. Berahas and Martin Takáč. SONIA: A Symmetric Blockwise Truncated Optimization Algorithm. 24th International Conference on Artificial Intelligence and Statistics (AISTATS), 2021, pp. 487-495. (Download PDF, Supplementary Material)
Talk
- (virtual) SIAM CSE 2021, SIAM Conference on Computational Science and Engineering, Fort Worth, TX.
Newton-Sketch and Subsampled Newton Methods
The concepts of sketching and subsampling have recently received much attention by the optimization and statistics communities. In this work, we study Newton-Sketch and Subsampled Newton (SSN) methods for the finite-sum optimization problem. We consider practical versions of the two methods in which the Newton equations are solved approximately using the conjugate gradient (CG) method or a stochastic gradient iteration. We establish new complexity results for the SSN-CG method that exploit the spectral properties of CG. Controlled numerical experiments compare the relative strengths of Newton-Sketch and SSN methods and show that for many finite-sum problems, they are far more efficient than SVRG, a popular first-order method.
Paper
- Albert S. Berahas, Raghu Bollapragada and Jorge Nocedal. An Investigation of Newton-Sketch and Subsampled Newton Methods. Optimization Methods and Software, 2020, 35(4), pp. 661–680. (Download PDF, OMS Online, Supplementary Material)
Talk
- SIOPT 2017, SIAM Conference on Optimization, Vancouver, Canada. (slides)
Robust Stochastic Quasi-Newton Methods for Machine Learning
The question of how to parallelize the stochastic gradient (SG) method has received much attention in the literature. In this work, we focus instead on batch methods that use a sizeable fraction of the training set at each iteration to facilitate parallelism, and that employ second-order information. We describe an implementation of the L-BFGS method designed to deal with two adversarial situations. The first occurs in distributed computing environments where some of the computational nodes devoted to the evaluation of the function and gradient are unable to return results on time. A similar challenge occurs in a multi-batch approach in which the data points used to compute the function and gradient are purposely changed at each iteration to accelerate the learning process. The aforementioned settings inherently give the algorithm a stochastic flavor that can cause instability in L-BFGS. These difficulties arise because L-BFGS employs gradient differences to update the Hessian approximations; when these gradients are computed using different data points the process can be unstable. This work shows how to perform stable quasi-Newton updating in the multi-batch setting, illustrates the behavior of the algorithm in a distributed computing platform on binary classification logistic regression and neural network training problems that arise in machine learning, and studies its convergence properties for both the convex and nonconvex cases.
Papers
- Albert S. Berahas and Martin Takáč, A Robust Multi-Batch L-BFGS Method for Machine Learning. Optimization Methods and Software, 2020, 35(1), pp. 191-219. (Download PDF, OMS Online, Supplementary Material)
- Albert S. Berahas, Jorge Nocedal and Martin Takáč, A Multi-Batch L-BFGS Method for Machine Learning. 2016 Advances In Neural Information Processing Systems (NeurIPS), Barcelona, Spain, Dec 2016, pp. 1055-1063. (Download PDF, Supplementary Material)
Talk
- CASSC 2017, SIAM Student Conference (Chicago area), Evanston, IL. (slides)
Stochastic Quasi-Newton Methods for Training Recurrent Neural Networks
Recurrent Neural Networks (RNNs) are powerful models that achieve exceptional performance on several pattern recognition problems. However, training of RNNs is a computationally difficult task owing to the well-known “vanishing/exploding” gradient problem. Algorithms proposed for training RNNs either exploit no (or limited) curvature information and have cheap per-iteration complexity, or attempt to gain significant curvature information at the cost of increased per-iteration cost. The former set includes diagonally-scaled first-order methods such as ADAM and ADAGRAD, while the latter consists of second-order algorithms like Hessian-Free Newton and K-FAC. In this work, we present adaQN, a stochastic quasi-Newton algorithm for training RNNs. Our approach retains a low per-iteration cost while allowing for non-diagonal scaling through a stochastic L-BFGS updating scheme. The method uses a novel L-BFGS scaling initialization scheme and is judicious in storing and retaining L-BFGS curvature pairs. We present numerical experiments on two language modeling tasks and show that adaQN is competitive with popular RNN training algorithms.
Paper
- Nitish Shirish Keskar and Albert S. Berahas, adaQN: An adaptive quasi-Newton algorithm for training RNNs. 2016 European Conference Machine Learning and Knowledge Discovery in Databases (ECML PKDD), Riva del Garda, Italy, Sept 2016, pp. 1-16. (Download PDF)
Talks
- ECML 2016, European Conference on Machine Learning, Riva del Garda, Italy. (slides)
- CASSC 2016, SIAM Student Conference (Chicago area), Chicago, IL. (slides)
Derivative-Free Optimization
Derivative-Free Optimization of Noisy Function via Quasi-Newton Methods
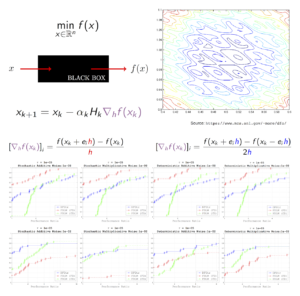
In this work, we present a finite difference quasi-Newton method for the minimization of noisy functions. The method takes advantage of the scalability and power of BFGS updating, and employs an adaptive procedure for choosing the differencing interval (h) based on the noise estimation techniques of Hamming (2012) and Moré and Wild (2011). This noise estimation procedure and the selection of h are inexpensive but not always accurate, and to prevent failures the algorithm incorporates a recovery mechanism that takes appropriate action in the case when the line search procedure is unable to produce an acceptable point. A novel convergence analysis is presented that considers the effect of a noisy line search procedure. Numerical experiments comparing the method to a model based trust region method are presented.
Paper
- Albert S. Berahas, Richard Byrd and Jorge Nocedal. Derivative-Free Optimization of Noisy Functions via Quasi-Newton Methods. SIAM Journal on Optimization, 2019, 29(2), pp. 965-993. (Download PDF, SIOPT Online)
Talks
- ISMP 2018, International Symposium on Mathematical Programming, Bordeaux, France. (slides)
- MOPTA 2018, Modeling and Optimization: Theory and Applications, Bethlehem, PA. (slides)
- INFORMS 2017, Institute for Operations Research and the Management Sciences Conference, Houston, TX. (slides)
Gradient Approximations in Derivative-Free Optimization
In this work, we analyze several methods for approximating the gradient of a function using only function values. These methods include finite differences, linear interpolation, Gaussian smoothing and smoothing on a unit sphere. The methods differ in the number of functions sampled, the choice of the sample points and the way in which the gradient approximations are derived. For each method, we derive bounds on the number of samples and the sampling radius which guarantee favorable convergence properties for a line search or fixed step size descent method. To this end, we derive one common condition on the accuracy of gradient approximations which guarantees these convergence properties and then show how each method can satisfy this condition. We analyze the convergence properties even when this condition is only satisfied with some sufficiently large probability at each iteration, as happens to be the case with Gaussian smoothing and smoothing on a unit sphere. Finally, we present numerical results evaluating the quality of the gradient approximations as well as their performance in conjunction with a line search derivative-free optimization algorithm.
Papers
- Albert S. Berahas, Liyuan Cao, Krzysztof Choromanski and Katya Scheinberg. A Theoretical and Empirical Comparison of Gradient Approximations in Derivative-Free Optimization. Foundations of Computational Mathematics, 2021, DOI: 10.1007/s10208-021-09513-z. (Download PDF, FoCM Online)
- Albert S. Berahas, Liyuan Cao, Krzysztof Choromanski and Katya Scheinberg. Linear interpolation gives better gradients than Gaussian smoothing in derivative-free optimization. Technical Report, Lehigh University 2019. (Download PDF)
Talk
- CSE 2019, SIAM Conference on Computational Science and Engineering, Spokane, WA. (slides)
Full-Low Evaluation Methods for Derivative-Free Optimization
We propose a new class of directional methods for Derivative-Free Optimization that considers two types of iterations. The first type is expensive in function evaluations, but exhibits good performance in the smooth, non-noisy case. The instance considered is BFGS computed over gradients approximated by finite differences. The second type is cheap in function evaluations, more appropriate under the presence of noise or non-smoothness. The instance considered is probabilistic direct search with 1 or 2 random directions.The resulting Full-Low Evaluation method is globally convergent even in the non-smooth case, and yields the appropriate rates in the smooth case. Preliminary results show that is efficient and robust across problems with different levels of smoothness and noise. Our approach can be extended to linear constraints using approximate tangent cones.
Paper
- (Status: Submitted) Albert S. Berahas, Oumaima Sohab, and Luis Nunes Vicente. Full-low evaluation methods for derivative-free optimization. arXiv preprint arXiv:2107.11908, 2021. (Download PDF)
Distributed Optimization
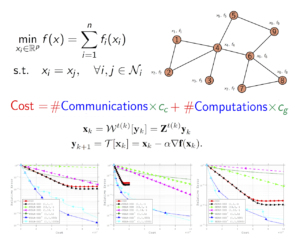
Communication and Computation Efficient Methods for Distributed Optimization
A distributed optimization method typically consists of two key components: communication and computation. The standard way of judging an algorithm via only the number of iterations overlooks the complexity associated with each iteration. Furthermore, various applications deploying distributed methods may prefer a different composition of communication and computation. Motivated by this discrepancy, in this work we propose an adaptive cost framework which adjusts the cost measure depending on the features of various applications. Moreover, we present a flexible algorithmic framework, where communication and computation steps are explicitly decomposed to enable algorithm customization for various applications. We apply this framework to the well-known distributed gradient descent (DGD) method, and develop a class of customized algorithms that compare favorably to their base algorithms, both theoretically and empirically. We test the performance and illustrate the flexibility of the methods on quadratic functions and classification problems that arise in machine learning, in terms of iterations, gradient evaluations, communications as well as the proposed cost framework.
Papers
- Albert S. Berahas, Raghu Bollapragada and Ermin Wei. On the Convergence of Nested Distributed Gradient Methods with Multiple Consensus and Gradient Steps. IEEE Transactions on Signal Processing, 2021, DOI: 10.1109/TSP.2021.3094906. (Download PDF, IEEE Xplore)
- Albert S. Berahas, Raghu Bollapragada, Nitish Shirish Keskar and Ermin Wei. Balancing Communication and Computation in Distributed Optimization. IEEE Transactions on Automatic Control, 2019, 64(8), pp. 3141-3155. (Download PDF, IEEE Xplore)
Talk
- IFORS 2017, International Federations on Operations Research Societies Conference, Quebec city, Canada. (slides)
Adaptive Methods with Quantized Communication
We consider the minimization of a sum of local convex objective functions in a distributed setting, where communication can be costly. We propose and analyze a class of nested distributed gradient methods with adaptive quantized communication. We show the effect of performing multiple quantized communication steps on the rate of convergence and on the size of the neighborhood of convergence, and prove R-Linear convergence to the exact solution with increasing number of consensus steps and adaptive quantization. We test the performance of the method, as well as some practical variants, on quadratic functions, and show the effects of multiple quantized communication steps in terms of iterations/gradient evaluations, communication and cost.
Paper
- Albert S. Berahas, Charikleia Iakovidou and Ermin Wei. Nested Distributed Gradient Methods with Adaptive Quantized Communication. 58th IEEE Conference on Decision and Control (CDC), Nice, France, 2019, pp. 1519-1525. (Download PDF, IEEE Xplore)
Applications of Machine Learning
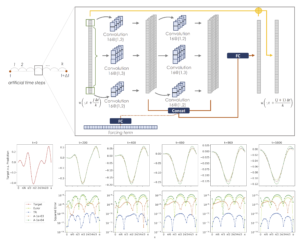
Fast Prediction of Partial Differential Equations
Discovering the underlying behavior of complex systems is an important topic in many science and engineering disciplines. In this paper, we propose a novel neural network framework, finite difference neural networks (FD-Net), to learn partial differential equations from data. Specifically, our proposed finite difference inspired network is designed to learn the underlying governing partial differential equations from trajectory data, and to iteratively estimate the future dynamical behavior using only a few trainable parameters. We illustrate the performance (predictive power) of our framework on the heat equation, with and without noise and/or forcing, and compare our results to the Forward Euler method. Moreover, we show the advantages of using a Hessian-Free Trust Region method to train the network.
Paper
- Zheng Shi, Nur Sila Gulgec, Albert S. Berahas, Shamim N. Pakzad, Martin Takáč. Finite Difference Neural Networks: Fast Prediction of Partial Differential Equations. 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA), 2020, pp. 130-135. (Download PDF)
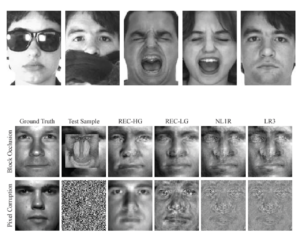
Face Recognition
We present work on two fronts: (1) a novel approach to face recognition, and (2) a general framework for robust error estimation in face recognition.
With regards to (1), we propose an adaptation and extension of the state-of-the-art methods in face recognition. Effectively, our method combines the sparsity-based approaches with additional least-squares steps and exhibits robustness to outliers achieving significant performance improvement with little additional cost. With regards to (2), we propose a general framework that allows the simultaneous use of various loss functions for modeling the residual in face images. Our method extends the current literature offering flexibility in the selection of the residual modeling characteristics but, at the same time, considering many existing algorithms as special cases.
Papers
- Michael Iliadis, Leonidas Spinoulas, Albert S. Berahas, Haohong Wang, and Aggelos K. Katsaggelos, Multi-model robust error correction for face recognition. 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, Arizona, Sept 2016, pp. 3229-3233. (IEEE Xplore)
- Michael Iliadis, Leonidas Spinoulas, Albert S. Berahas, Haohong Wang, and Aggelos K. Katsaggelos, Sparse representation and least squares-based classification in face recognition. 2014 IEEE 22nd European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, Sept 2014, pp. 526-530. (IEEE Xplore)
Other Applications
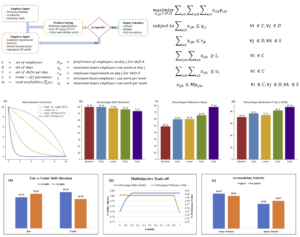
Auction-Based Preferential Shift Scheduling: A Case Study on the Lehigh University Libraries
Shift Scheduling is an important problem as employee satisfaction has become an essential aspect for every organization. We tackle a variant of this problem that prioritizes employee preferences for shift assignment subject to a set of employer-specific constraints. Employee preference is an important feature of our study and hence we discuss the effect of preference quantification via different normalization schemes. Furthermore, we develop a multi-objective integer programming model that analyzes the trade-off between preference maximization and maximum shift assignment. We validate our methodology using real data obtained from work-study students at the Lehigh University libraries. Our results indicate that the proposed models provide solutions that balance preference maximization and shift assignment. Finally, we mention that our model was used to staff the Lehigh University libraries in Spring 2020.
Paper
- Sudeep Metha, Ved Patel and Albert S. Berahas. Auction-Based Preferential Shift Scheduling: A Case Study on the Lehigh University Libraries. Institute of Industrial and Systems Engineers (IISE) Conference and Expo, 2021. (Download PDF)